Running Storm on Parametric Models
Many model descriptions contain constants which may be specified only by an interval of possible values. We refer to these constants as parameters. Such parametric models are supported by the binary storm-pars. A gentle overview is given in [1].
Overall, for parametric systems, various questions (henceforth: queries) relating to model checking can be asked. These different queries are supported by different engines in storm-pars: We refer to this as the mode – and the mode must always be specified.
The current support focusses on five modes, of which two are more experimental:
- Feasibility – Finding parameter values such that a property holds.
- Verification – Proving that for all parameter values in some region, a property holds.
- Partitioning – Finding regions for which the verification problem holds.
- Solution Function computation – Finding a closed-form representation of a solution function, mapping parameter values to, e.g., reachability probabilities.
- Monotonicity analysis (experimental) – Checking whether the solution function is monotonic in one of the parameters.
- Sampling (experimental) – Quickly sampling parametric models for different parameter valuations.
We outline these modes in more detail below. In what follows, Storm typically assumes that all occurring parameters are graph-preserving, that is, they do not influence the topology of the underlying Markov model.
To illustrate the functionality, we use a bounded retransmission protocol. This example is an adaption of the Bounded Retransmission Protocol from the PRISM website. Here, we have two channels whose reliabilities are represented by parameters pL and pK.
Download parametric version of the Bounded Retransmission Protocol
// bounded retransmission protocol [D'AJJL01]
// gxn/dxp 23/05/2001
dtmc
// number of chunks
const int N = 2;
// maximum number of retransmissions
const int MAX = 4;
// reliability of channels
const double pL;
const double pK;
// timeouts
const double TOMsg = 0.1;
const double TOAck = 0.1;
module sender
s : [0..6];
// 0 idle
// 1 next_frame
// 2 wait_ack
// 3 retransmit
// 4 success
// 5 error
// 6 wait sync
srep : [0..3];
// 0 bottom
// 1 not ok (nok)
// 2 do not know (dk)
// 3 ok (ok)
nrtr : [0..MAX];
i : [0..N];
bs : bool;
s_ab : bool;
fs : bool;
ls : bool;
// idle
[NewFile] (s=0) -> (s'=1) & (i'=1) & (srep'=0);
// next_frame
[aF] (s=1) -> (s'=2) & (fs'=(i=1)) & (ls'=(i=N)) & (bs'=s_ab) & (nrtr'=0);
// wait_ack
[aB] (s=2) -> (s'=4) & (s_ab'=!s_ab);
[TO_Msg] (s=2) -> (s'=3);
[TO_Ack] (s=2) -> (s'=3);
// retransmit
[aF] (s=3) & (nrtr<MAX) -> (s'=2) & (fs'=(i=1)) & (ls'=(i=N)) & (bs'=s_ab) & (nrtr'=nrtr+1);
[] (s=3) & (nrtr=MAX) & (i<N) -> (s'=5) & (srep'=1);
[] (s=3) & (nrtr=MAX) & (i=N) -> (s'=5) & (srep'=2);
// success
[] (s=4) & (i<N) -> (s'=1) & (i'=i+1);
[] (s=4) & (i=N) -> (s'=0) & (srep'=3);
// error
[SyncWait] (s=5) -> (s'=6);
// wait sync
[SyncWait] (s=6) -> (s'=0) & (s_ab'=false);
endmodule
module receiver
r : [0..5];
// 0 new_file
// 1 fst_safe
// 2 frame_received
// 3 frame_reported
// 4 idle
// 5 resync
rrep : [0..4];
// 0 bottom
// 1 fst
// 2 inc
// 3 ok
// 4 nok
fr : bool;
lr : bool;
br : bool;
r_ab : bool;
recv : bool;
// new_file
[SyncWait] (r=0) -> (r'=0);
[aG] (r=0) -> (r'=1) & (fr'=fs) & (lr'=ls) & (br'=bs) & (recv'=Tvar);
// fst_safe_frame
[] (r=1) -> (r'=2) & (r_ab'=br);
// frame_received
[] (r=2) & (r_ab=br) & (fr=true) & (lr=false) -> (r'=3) & (rrep'=1);
[] (r=2) & (r_ab=br) & (fr=false) & (lr=false) -> (r'=3) & (rrep'=2);
[] (r=2) & (r_ab=br) & (fr=false) & (lr=true) -> (r'=3) & (rrep'=3);
[aA] (r=2) & !(r_ab=br) -> (r'=4);
// frame_reported
[aA] (r=3) -> (r'=4) & (r_ab'=!r_ab);
// idle
[aG] (r=4) -> (r'=2) & (fr'=fs) & (lr'=ls) & (br'=bs) & (recv'=Tvar);
[SyncWait] (r=4) & (ls=true) -> (r'=5);
[SyncWait] (r=4) & (ls=false) -> (r'=5) & (rrep'=4);
// resync
[SyncWait] (r=5) -> (r'=0) & (rrep'=0);
endmodule
// prevents more than one file being sent
module tester
Tvar : bool;
[NewFile] (Tvar=false) -> (Tvar'=true);
endmodule
module channelK
k : [0..2];
// idle
[aF] (k=0) -> pK : (k'=1) + 1-pK : (k'=2);
// sending
[aG] (k=1) -> (k'=0);
// lost
[TO_Msg] (k=2) -> (k'=0);
endmodule
module channelL
l : [0..2];
// idle
[aA] (l=0) -> pL : (l'=1) + 1-pL : (l'=2);
// sending
[aB] (l=1) -> (l'=0);
// lost
[TO_Ack] (l=2) -> (l'=0);
endmodule
label "error" = s=5;
rewards
[TO_Msg] true : TOMsg;
[TO_Ack] true : TOAck;
endrewards
Feasibility
Storm currently supports two feasibility engines:
- Parameter lifting, or just pla
- Gradient Descent, or just gd
While we work towards a unified interface, these support different options.
Feasibility with pla
The pla engine is based on work in [2]. The feasibility computation is partially based on work in [3].
$ storm-pars --mode feasibility --feasibility:method pla --prism brp.pm --prop 'P<=0.01 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
We use the --regions option to set the parameter region. In this case, the equivalent region could have been given using the --regionbound 0.1, which restricts every parameter to be bounded between regionbound and 1-regionbound.
The complete output to be expected is:
bin/storm-pars --mode feasibility --feasibility:method pla --prism brp.pm --prop 'P<=0.01 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
Storm-pars 1.8.2 (dev)
Date: Sat Nov 11 20:56:08 2023
Command line arguments: --mode feasibility '--feasibility:method' pla --prism brp.pm --prop 'P<=0.01 [F s=5]' --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9'
Current working directory: ~/storm/build
Time for model input parsing: 0.009s.
Time for model construction: 0.063s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model simplification: 0.003s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.004s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Find feasible solution for P=? [F (s = 5)] within region 1/10<=pK<=9/10,1/10<=pL<=9/10;
Result at initial state: 947822915828163/288230376151711744 ( approx. 0.003288421326) at [pK=17/20, pL=17/20].
Time for model checking: 0.005s.
In particular, the output says
Result at initial state: 947822915828163/288230376151711744 ( approx. 0.003288421326) at [pK=17/20, pL=17/20].
which means that setting pK and pL to 17/20 yields a Markov chain such that P<=0.01 [F s=5] is satisfied.
Instead of giving a bound, pla also support optimization:
$ storm-pars --mode feasibility --feasibility:method pla --prism brp.pm --prop 'P=? [F s=5]' --direction min --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9" --guarantee 0.0001 abs
In this case, we do not give a bound and specify with --direction min that we want to minimize the reachability probability.
Additionally, we give a --guarantee 0.0001 abs, specifying that we want to find a solution which is within 0.0001 of the optimal value, where the distance is measured in absolute terms.
The complete output to be expected is:
./storm-pars --mode feasibility --feasibility:method pla --prism brp.pm --prop 'P=? [F s=5]' --direction min --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9" --guarantee 0.0001 abs
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode feasibility '--feasibility:method' pla --prism brp.pm --prop 'P=? [F s=5]' --direction min --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9' --guarantee 0.0001 abs
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.011s.
Time for model construction: 0.065s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model simplification: 0.005s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.005s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Find feasible solution for P=? [F (s = 5)] within region 1/10<=pK<=9/10,1/10<=pL<=9/10;
Result at initial state: 5282881788238101/9223372036854775808 ( approx. 0.0005727711912) at [pK=287/320, pL=287/320].
Time for model checking: 0.008s.
In particular, the output says
Result at initial state: 5282881788238101/9223372036854775808 ( approx. 0.0005727711912) at [pK=287/320, pL=287/320].
This output indicates not only how to instantiate pK and pL to obtain P=? [F s=5] = approx. 0.0005727711912, but also that this value is within 0.0001 from the absolute lower bound (within the given region).
Feasibility with gd
The gd engine is based on work in [4].
$ storm-pars --mode feasibility --feasibility:method gd --prism brp.pm --prop 'P<=0.01 [F s=5]'
In this case, the region for searching cannot be given.
The complete output to be expected is:
bin/storm-pars --mode feasibility --feasibility:method pla --prism brp.pm --prop 'P<=0.01 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
Storm-pars 1.8.2 (dev)
Date: Sat Nov 11 20:56:08 2023
Command line arguments: --mode feasibility '--feasibility:method' pla --prism brp.pm --prop 'P<=0.01 [F s=5]' --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9'
Current working directory: ~/storm/build
Time for model input parsing: 0.009s.
Time for model construction: 0.063s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model simplification: 0.003s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.004s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Find feasible solution for P=? [F (s = 5)] within region 1/10<=pK<=9/10,1/10<=pL<=9/10;
Result at initial state: 947822915828163/288230376151711744 ( approx. 0.003288421326) at [pK=17/20, pL=17/20].
Time for model checking: 0.005s.
In particular, the output says
Result at initial state: 0.001706273496 ( approx. 0.001706273496) at [pK=62679533432486317/72057594037927936, pL=62679533432486317/72057594037927936].
which gives values for pK and pL such that P<=0.01 [F s=5] is satisfied.
Verification
To prove the absence of a solution, we can use parameter lifting. A comprehensive overview on the theoretical backgrounds is given in [2].
$ storm-pars --mode verification --prism brp.pm --prop 'P<=0.9999 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
will provide output
./storm-pars --mode verification --prism brp.pm --prop 'P<=0.9999 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode verification --prism brp.pm --prop 'P<=0.9999 [F s=5]' --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9'
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.001s.
Time for model construction: 0.013s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Formula is satisfied by all parameter instantiations.
Time for model checking: 0.007s.
➜ bin git:(pars-cli) ✗ ./storm-pars --mode verification --prism brp.pm --prop 'P<=0.9999 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
In contrast, running
$ storm-pars --mode verification --prism brp.pm --prop 'P<=0.99 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
will yield output that says that the statement is not true:
./storm-pars --mode verification --prism brp.pm --prop 'P<=0.99 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode verification --prism brp.pm --prop 'P<=0.99 [F s=5]' --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9'
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.008s.
Time for model construction: 0.049s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Formula is not satisfied by all parameter instantiations.
Time for model checking: 0.011s.
To find a counterexample, one can use the feasibility mode above.
Parameter Space Partitioning
The verification result may be too coarse: Potentially, we do want to find subregions that satisfy the property. While we generally advocate to use our (Python) API for flexible support of such scenarios, the Storm command-line interface does yield some support:
$ storm-pars --mode partitioning --prism brp.pm --prop 'P<=0.99 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
This produces the following output:
./storm-pars --mode partitioning --prism brp.pm --prop 'P<=0.99 [F s=5]' --region "0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9"
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode partitioning --prism brp.pm --prop 'P<=0.99 [F s=5]' --region '0.1 <= pL <= 0.9, 0.1 <= pK <= 0.9'
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.009s.
Time for model construction: 0.048s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Analyzing parameter region 1/10<=pK<=9/10,1/10<=pL<=9/10; using Parameter Lifting with iterative refinement until 95% is covered.
Model checking property "1": P<=99/100 [F (s = 5)] ...
Result (initial states): Fraction of satisfied area: 95.3125%
Fraction of unsatisfied area: 0%
Unknown fraction: 4.6875%
Total number of regions: 19
Unknown: 12
AllSat: 7
Region refinement Check result (visualization):
x-axis: pK y-axis: pL S=safe, [ ]=unsafe, -=ambiguous
##################################################################################################################################
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#----------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
#--------------------------------SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS#
##################################################################################################################################
Time for model checking: 0.009s.
We can see that for two parameters, Storm even visulalizes the acquired data to give an initial understanding of the region partition. To cover more (or less) parts of the parameter space, use --partitioning:terminationCondition 0.01 to say that 99% of the parameter space should be covered.
Computing the exact solution function
We can run Storm to obtain closed-form solutions, i.e. a rational function that represents, e.g., the probability with which the given property is satisfied for certain parameter valuations. A comprehensive overview on the theoretical backgrounds is given in [2].
$ storm-pars --mode solutionfunction --prism brp.pm --prop 'P=? [F s=5]'
The result is an expression over the parameter pL and pK:
(-1 * (pK^10*pL^10+(-120)*pK^7*pL^7+(-10)*pK^9*pL^9+45*pK^8*pL^8+210*pK^6*pL^6+(-250)*pK^5*pL^5+(-100)*pK^3*pL^3+25*pK^2*pL^2+200*pK^4*pL^4+(-1)))/(1)
./storm-pars --mode solutionfunction --prism brp.pm --prop 'P=? [F s=5]'
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode solutionfunction --prism brp.pm --prop 'P=? [F s=5]'
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.009s.
Time for model construction: 0.052s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Model checking property "1": P=? [F (s = 5)] ...
Result (initial states): (-1 * (pK^10*pL^10+(-120)*pK^7*pL^7+(-10)*pK^9*pL^9+45*pK^8*pL^8+210*pK^6*pL^6+(-250)*pK^5*pL^5+(-100)*pK^3*pL^3+25*pK^2*pL^2+200*pK^4*pL^4+(-1)))/(1)
Time for model checking: 0.006s.
Monotonicity analysis
Storm can also check if the parameters of a model are monotonic in regard to a certain property [5], [3]. For this, we use the monotonicity mode.
$ ./storm-pars --mode monotonicity --prism brp.pm --prop 'P=? [F s=5]' --bisimulation
We use --bisimulation to apply further model simplification and significantly reduce the workload of the model checker.
This results in the following output:
./storm-pars --mode monotonicity --prism brp.pm --prop 'P=? [F s=5]' --bisimulation
Storm-pars 1.8.2 (dev)
Date: Sun Nov 12 2023
Command line arguments: --mode monotonicity --prism brp.pm --prop 'P=? [F s=5]' --bisimulation
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.002s.
Time for model construction: 0.018s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 135
Transitions: 175
Reward Models: none
State Labels: 3 labels
* deadlock -> 5 item(s)
* init -> 1 item(s)
* (s = 5) -> 4 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model simplification: 0.000s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 43
Transitions: 83
Reward Models: none
State Labels: 4 labels
* target -> 1 item(s)
* init -> 1 item(s)
* deadlock -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.001s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 23
Transitions: 43
Reward Models: none
State Labels: 2 labels
* init -> 1 item(s)
* (s = 5) -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Number of done states: 23
No Assumptions
Monotonicity Result:
#Incr: 0 #Decr: 2
pK MonDecr; pL MonDecr;
Total time for monotonicity checking: 0.000s.
In particular, the output specifies that both pL and pK are monotonically decreasing.
If we want to take a look at the reachability order that is built during monotonicity checking, we can add the option --mon:dotOutput followed by an optional filename. Storm will then write a dot output of the order into the file which can then be processed using, e.g., Graphviz. In this case, it results in the following graph:
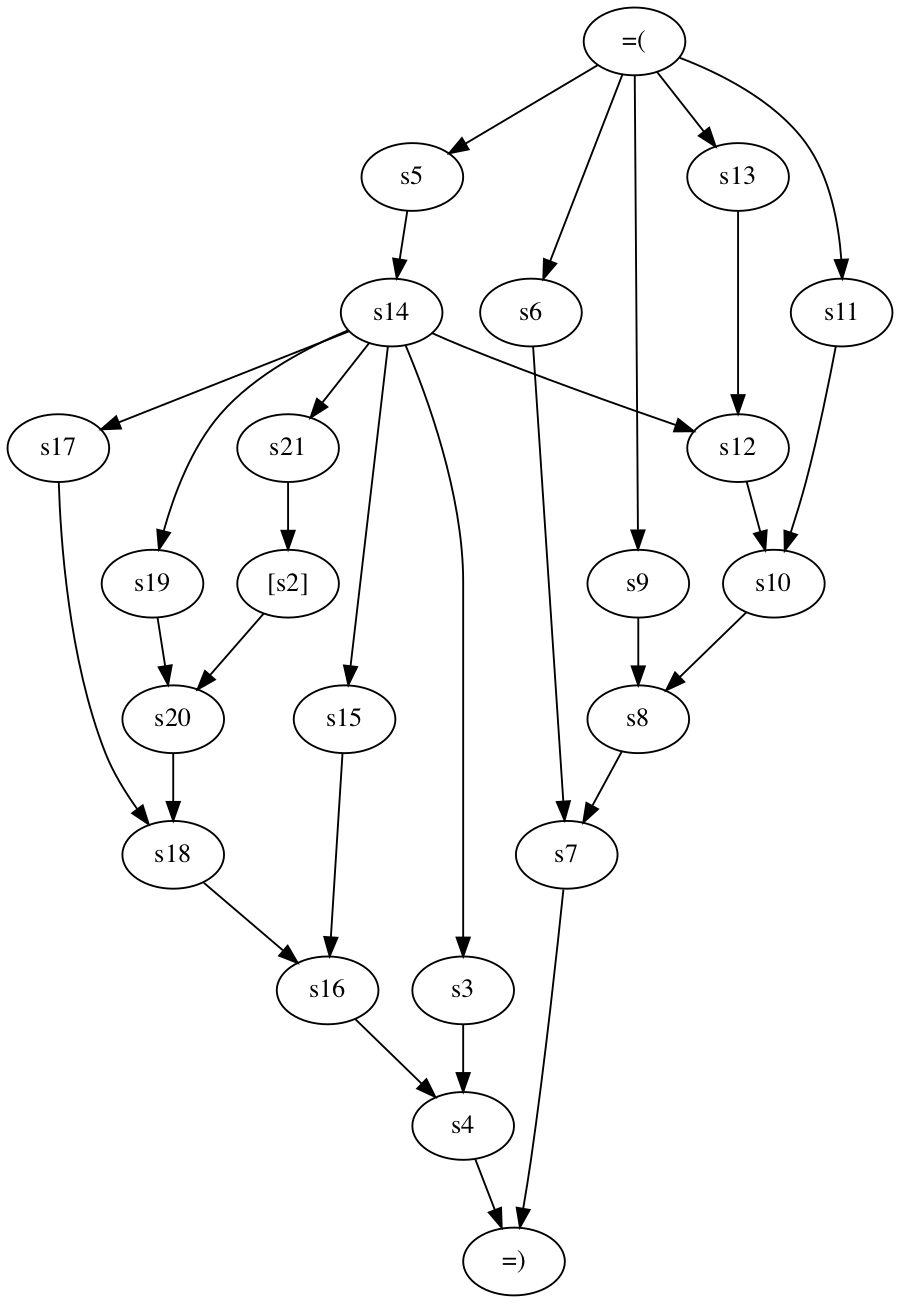
References
- Nils Jansen, Sebastian Junges, and Joost-Pieter Katoen, “Parameter Synthesis in Markov Models: A Gentle Survey,” in Principles of Systems Design, 2022.
- Sebastian Junges et al., “Parameter synthesis for Markov models: covering the parameter space,” Formal Methods Syst. Des., no. 1, 2024.
- Jip Spel, Sebastian Junges, and Joost-Pieter Katoen, “Finding Provably Optimal Markov Chains,” in TACAS, 2021.
- Linus Heck, Jip Spel, Sebastian Junges, Joshua Moerman, and Joost-Pieter Katoen, “Gradient-Descent for Randomized Controllers Under Partial Observability,” in VMCAI, 2022.
- Jip Spel, Sebastian Junges, and Joost-Pieter Katoen, “Are Parametric Markov Chains Monotonic?,” in ATVA, 2019.


