Running Storm
- Storm’s executables
- First steps
- Running Storm on PRISM, JANI or explicit input
- Running Storm on GSPNs
Storm’s executables
Storm takes many languages as input. For some of these formats, domain-specific information is available and domain-specific properties are of key importance. Others are generic and require more flexibility in terms of options. As a result, there are several binaries that are each dedicated to a specific portion of the input languages. The following table gives an overview of the available executables, the targets that need to be built when compiling Storm from source and the documentation for each executable.
| input language(s) | executable | make target | Documentation |
| PRISM, JANI, explicit | storm | storm-cli | Running Storm on PRISM, JANI or explicit input |
| PRISM, JANI, explicit | storm-pars | storm-pars-cli | Running Storm on parametric models |
| DFTs | storm-dft | storm-dft-cli | Running Storm on DFTs |
| GSPNs | storm-gspn | storm-gspn-cli | Running Storm on GSPNs |
Consequently, our guide on how to run Storm is structured accordingly. For every executable we illustrate the usage by one (or more) example(s).
First steps
Many of Storm’s executables have many options, only a fraction of which are covered in this guide. If you want to explore these options, invoke the executable with the --help [hint] option. If a hint is given, only those options are shown that match it.
Before we get started, let us check whether everything is set up properly. In all command-line examples we assume that the executables are in your PATH and can therefore be invoked without prefixing them with their path. If you installed Storm via Homebrew, this is automatically the case; if you built Storm yourself, you have to manually add it to your PATH. Typing
$ storm
should produce output similar to
Storm 1.0.0
ERROR (cli.cpp:309): No input model.
ERROR (storm.cpp:39): An exception caused Storm to terminate. The message of the exception is: No input model.
Of course your version may differ, but the general picture should be the same. In particular, storm should complain about a missing input model. More information about the Storm version can be obtained by providing --version.
Running Storm on PRISM, JANI or explicit input
These input languages can be treated by Storm’s main executable storm. Storm supports various properties. They can be passed to Storm by providing the --prop <properties> <selection> switch. The <properties> argument can be either a property as a string or the path to a file containing the properties. The <selection> argument is optional. If set, it can be used to indicate that only certain properties of the provided ones are to be checked. More specifically, this argument is either “all” or a comma-separated list of names of properties and/or property indices. Note that named properties cannot be indexed by name, but need to be referred to by their name.
Running Storm on PRISM input
PRISM models can be provided with the --prism <path/to/prism-file> option.
Example 1 (Analysis of a PRISM model of the Knuth-Yao die)
In our first example, we are going to analyze a small DTMC in the PRISM format. More specifically, the model represents a protocol to simulate a six-sided die with the use of a fair coin only. The model and more information can be found at the PRISM website, but for your convenience, you can view the model and the download link below.
Download PRISM model of Knuth-Yao die
// Knuth's model of a fair die using only fair coins
dtmc
module die
// local state
s : [0..7] init 0;
// value of the dice
d : [0..6] init 0;
[] s=0 -> 0.5 : (s'=1) + 0.5 : (s'=2);
[] s=1 -> 0.5 : (s'=3) + 0.5 : (s'=4);
[] s=2 -> 0.5 : (s'=5) + 0.5 : (s'=6);
[] s=3 -> 0.5 : (s'=1) + 0.5 : (s'=7) & (d'=1);
[] s=4 -> 0.5 : (s'=7) & (d'=2) + 0.5 : (s'=7) & (d'=3);
[] s=5 -> 0.5 : (s'=7) & (d'=4) + 0.5 : (s'=7) & (d'=5);
[] s=6 -> 0.5 : (s'=2) + 0.5 : (s'=7) & (d'=6);
[] s=7 -> (s'=7);
endmodule
rewards "coin_flips"
[] s<7 : 1;
endrewards
From now on, we will assume that the model file is stored as die.pm in the current directory. Let us start with a simple (exhaustive) exploration of the state space of the model:
$ storm --prism die.pm
Storm 1.0.0
Command line arguments: --prism die.pm
Current working directory: ~/storm/build/bin
Time for model construction: 0.287s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: none
Labels: 2
* deadlock -> 0 state(s)
* init -> 1 state(s)
choice labels: no
--------------------------------------------------------------
This will tell you that the model is a sparse discrete-time Markov chain with 13 states and 20 transitions, no reward model and two labels (deadlock and init). But wait, doesn’t the PRISM model actually specify a reward model? Why does storm not find one? The reason is simple, storm doesn’t build reward models or (custom) labels that are not referred to by properties unless you explicitly want all of them to be built:
$ storm --prism die.pm --buildfull
Storm 1.0.0
Command line arguments: --prism die.pm --buildfull
Current working directory: ~/storm/build/bin
Time for model construction: 0.291s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: coin_flips
Labels: 2
* deadlock -> 0 state(s)
* init -> 1 state(s)
choice labels: no
--------------------------------------------------------------
This gives you the same model, but this time there is a reward model coin_flips attached to it. Unless you want to know how many states satisfy a custom label, you can let storm take care of generating the needed reward models and labels. Note that by default, the model is stored in an sparse matrix representation (hence the (sparse) marker after the model type). There are other formats supported by Storm; please look at the engines guide for more details.
Now, let’s say we want to check whether the probability to roll a one with our simulated die is as we’d expect. As the protocol states the simulated die shows a one if it ends up in a state where s=7&d=1, we formulate a reachability property like this:
$ storm --prism die.pm --prop "P=? [F s=7&d=1]"
Storm 1.0.0
Command line arguments: --prism die.pm --prop P=? [F s=7&d=1]
Current working directory: ~/storm/build/bin
Time for model construction: 0.292s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: none
Labels: 3
* deadlock -> 0 state(s)
* init -> 1 state(s)
* ((s = 7) & (d = 1)) -> 1 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property P=? [F ((s = 7) & (d = 1))] ...
Result (initial states): 0.1666666667
Time for model checking: 0.003s.
This will tell us that the probability for rolling a one is actually (very close to) 1/6.
If, from the floating point figure, you are not convinced that the result is actually 1 over 6, try to additionally provide the --exact flag.
Congratulations, you have now checked your first property with Storm! Now, say we are interested in the probability of rolling a one, provided that one of the outcomes “one”, “two” or “three” were obtained, we can obtain this figure by using a conditional probability formula like this
$ storm --prism die.pm --prop "P=? [F s=7&d=1 || F s=7&d<4]"
Storm 1.0.0
Command line arguments: --prism die.pm --prop P=? [F s=7&d=1 || F s=7&d<4]
Current working directory: ~/storm/build/bin
Time for model construction: 0.294s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: none
Labels: 4
* deadlock -> 0 state(s)
* init -> 1 state(s)
* ((s = 7) & (d = 1)) -> 1 state(s)
* ((s = 7) & (d < 4)) -> 3 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property P=? [F ((s = 7) & (d = 1)) || F ((s = 7) & (d < 4))] ...
Result (initial states): 0.3333333333
Time for model checking: 0.001s.
which tells us that this probability is 1/3. So far the model seems to simulate a proper six-sided die! Finally, we are interested in the expected number of coin flips that need to be made until the simulated die returns an outcome:
$ storm --prism die.pm --prop "R{\"coin_flips\"}=? [F s=7]"
Storm 1.0.0
Command line arguments: --prism die.pm --prop R{"coin_flips"}=? [F s=7]
Current working directory: ~/storm/build/bin
Time for model construction: 0.286s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: coin_flips
Labels: 3
* deadlock -> 0 state(s)
* init -> 1 state(s)
* (s = 7) -> 6 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property R[exp]{"coin_flips"}=? [F (s = 7)] ...
Result (initial states): 3.666666667
Time for model checking: 0.000s.
storm tells us that – on average – we will have to flip our fair coin 11/3 times. Note that we had to escape the quotes around the reward model name in the property string. If the property is placed within a file, there is no need to escape them.
More information on how to define properties can be found here.
Example 2 (Analysis of a PRISM model of an asynchronous leader election protocol)
In this example, we consider another model available from the PRISM website: the asynchronous leader election protocol.
Download PRISM model of asynchronous leader election protocol
// asynchronous leader election
// 4 processes
// gxn/dxp 29/01/01
mdp
const N=4; // number of processes
module process1
// COUNTER
c1 : [0..N-1];
// STATES
s1 : [0..4];
// 0 make choice
// 1 have not received neighbours choice
// 2 active
// 3 inactive
// 4 leader
// PREFERENCE
p1 : [0..1];
// VARIABLES FOR SENDING AND RECEIVING
receive1 : [0..2];
// not received anything
// received choice
// received counter
sent1 : [0..2];
// not send anything
// sent choice
// sent counter
// pick value
[] (s1=0) -> 0.5 : (s1'=1) & (p1'=0) + 0.5 : (s1'=1) & (p1'=1);
// send preference
[p12] (s1=1) & (sent1=0) -> (sent1'=1);
// receive preference
// stay active
[p41] (s1=1) & (receive1=0) & !( (p1=0) & (p4=1) ) -> (s1'=2) & (receive1'=1);
// become inactive
[p41] (s1=1) & (receive1=0) & (p1=0) & (p4=1) -> (s1'=3) & (receive1'=1);
// send preference (can now reset preference)
[p12] (s1=2) & (sent1=0) -> (sent1'=1) & (p1'=0);
// send counter (already sent preference)
// not received counter yet
[c12] (s1=2) & (sent1=1) & (receive1=1) -> (sent1'=2);
// received counter (pick again)
[c12] (s1=2) & (sent1=1) & (receive1=2) -> (s1'=0) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0);
// receive counter and not sent yet (note in this case do not pass it on as will send own counter)
[c41] (s1=2) & (receive1=1) & (sent1<2) -> (receive1'=2);
// receive counter and sent counter
// only active process (decide)
[c41] (s1=2) & (receive1=1) & (sent1=2) & (c4=N-1) -> (s1'=4) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0);
// other active process (pick again)
[c41] (s1=2) & (receive1=1) & (sent1=2) & (c4<N-1) -> (s1'=0) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0);
// send preference (must have received preference) and can now reset
[p12] (s1=3) & (receive1>0) & (sent1=0) -> (sent1'=1) & (p1'=0);
// send counter (must have received counter first) and can now reset
[c12] (s1=3) & (receive1=2) & (sent1=1) -> (s1'=3) & (p1'=0) & (c1'=0) & (sent1'=0) & (receive1'=0);
// receive preference
[p41] (s1=3) & (receive1=0) -> (p1'=p4) & (receive1'=1);
// receive counter
[c41] (s1=3) & (receive1=1) & (c4<N-1) -> (c1'=c4+1) & (receive1'=2);
// done
[done] (s1=4) -> (s1'=s1);
// add loop for processes who are inactive
[done] (s1=3) -> (s1'=s1);
endmodule
module process2=process1[s1=s2,p1=p2,c1=c2,sent1=sent2,receive1=receive2,p12=p23,p41=p12,c12=c23,c41=c12,p4=p1,c4=c1] endmodule
module process3=process1[s1=s3,p1=p3,c1=c3,sent1=sent3,receive1=receive3,p12=p34,p41=p23,c12=c34,c41=c23,p4=p2,c4=c2] endmodule
module process4=process1[s1=s4,p1=p4,c1=c4,sent1=sent4,receive1=receive4,p12=p41,p41=p34,c12=c41,c41=c34,p4=p3,c4=c3] endmodule
// reward - expected number of rounds (equals the number of times a process receives a counter)
rewards "rounds"
[c12] true : 1;
endrewards
Just like in Example 1, we will assume that the file leader4.nm is located in the current directory.
As the name of the protocol suggests, it is supposed to elect a leader among a set of communicating agents (four in this particular instance). Well, let’s see whether it lives up to it’s name and check that almost surely (i.e. with probability 1) a leader will be elected eventually.
$ storm --prism leader4.nm --prop "P>=1 [F (s1=4 | s2=4 | s3=4 | s4=4) ]"
Storm 1.0.0
Command line arguments: --prism leader4.nm --prop P>=1 [F (s1=4 | s2=4 | s3=4 | s4=4) ]
Current working directory: ~/storm/build/bin
Time for model construction: 0.403s.
--------------------------------------------------------------
Model type: MDP (sparse)
States: 3172
Transitions: 7144
Choices: 6252
Reward Models: none
Labels: 3
* deadlock -> 0 state(s)
* init -> 1 state(s)
* ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4)) -> 4 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property P>=1 [F ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4))] ...
Result (initial states): true
Time for model checking: 0.008s.
Apparently this is true. But what about the performance of the protocol? The property we just checked does not guarantee any upper bound on the number of steps that we need to make until a leader is elected. Suppose we have only 40 steps and want to know what’s the probability to elect a leader within this time bound.
$ storm --prism leader4.nm --prop "P=? [F<=40 (s1=4 | s2=4 | s3=4 | s4=4) ]"
Storm 1.0.0
Command line arguments: --prism leader4.nm --prop P=? [F<=40 (s1=4 | s2=4 | s3=4 | s4=4) ]
Current working directory: ~/storm/build/bin
Time for model construction: 0.395s.
--------------------------------------------------------------
Model type: MDP (sparse)
States: 3172
Transitions: 7144
Choices: 6252
Reward Models: none
Labels: 3
* deadlock -> 0 state(s)
* init -> 1 state(s)
* ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4)) -> 4 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property P=? [true U<=40 ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4))] ...
ERROR (SparseMdpPrctlModelChecker.cpp:60): Formula needs to specify whether minimal or maximal values are to be computed on nondeterministic model.
ERROR (storm.cpp:39): An exception caused Storm to terminate. The message of the exception is: Formula needs to specify whether minimal or maximal values are to be computed on nondeterministic model.
Likely, Storm will tell you that there is an error and that for nondeterministic models you need to specify whether minimal or maximal probabilities are to be computed. Why is that? Since the model is a Markov Decision Process, there are (potentially) nondeterministic choices in the model that need to be resolved. Storm doesn’t know how to resolve them unless you tell it to either minimize or maximize (w.r.t. the probability of the objective) whenever there is a nondeterministic choice.
$ storm --prism leader4.nm --prop "Pmin=? [F<=40 (s1=4 | s2=4 | s3=4 | s4=4) ]"
Storm 1.0.0
Command line arguments: --prism leader4.nm --prop Pmin=? [F<=40 (s1=4 | s2=4 | s3=4 | s4=4) ]
Current working directory: ~/storm/build/bin
Time for model construction: 0.393s.
--------------------------------------------------------------
Model type: MDP (sparse)
States: 3172
Transitions: 7144
Choices: 6252
Reward Models: none
Labels: 3
* deadlock -> 0 state(s)
* init -> 1 state(s)
* ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4)) -> 4 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property Pmin=? [true U<=40 ((((s1 = 4) | (s2 = 4)) | (s3 = 4)) | (s4 = 4))] ...
Result (initial states): 0.3828125
Time for model checking: 0.030s.
Storm should tell you that this probability is 0.3828125. So what does it mean? It means that even in the worst of all cases, so when every nondeterministic choice in the model is chosen to minimize the probability to elect a leader quickly, then we will elect a leader within our time bound in about 49 out of 128 cases.
For nondeterministic models (MDPs and MAs), you will have to specify in which direction the nondeterminism is going to be resolved.
Multi-objective Model Checking of MDPs and Markov Automata
Storm supports multi-objective model checking: In nondeterministic models, different objectives might require different choices of actions in order to satisfy the property. This induces trade-offs between different strategies. Multi-objective model checking reveals such trade-offs by computing the Pareto curve. An example is given below.
Example 3 (Pareto Curves)
Consider an instance of stochastic job scheduling, where a number of jobs with exponential run time needs to be handled by a number of servers. On one hand, we are interested in reducing the expected time until all jobs are done. On the other hand, we want to maximize the probability that a first batch of jobs has been treated within an hour. This yields a trade-off, as the optimal strategy for minimizing the expected time is to run the slowest jobs first.
The trade-off for 12 jobs and 3 servers is depicted by the following curve:
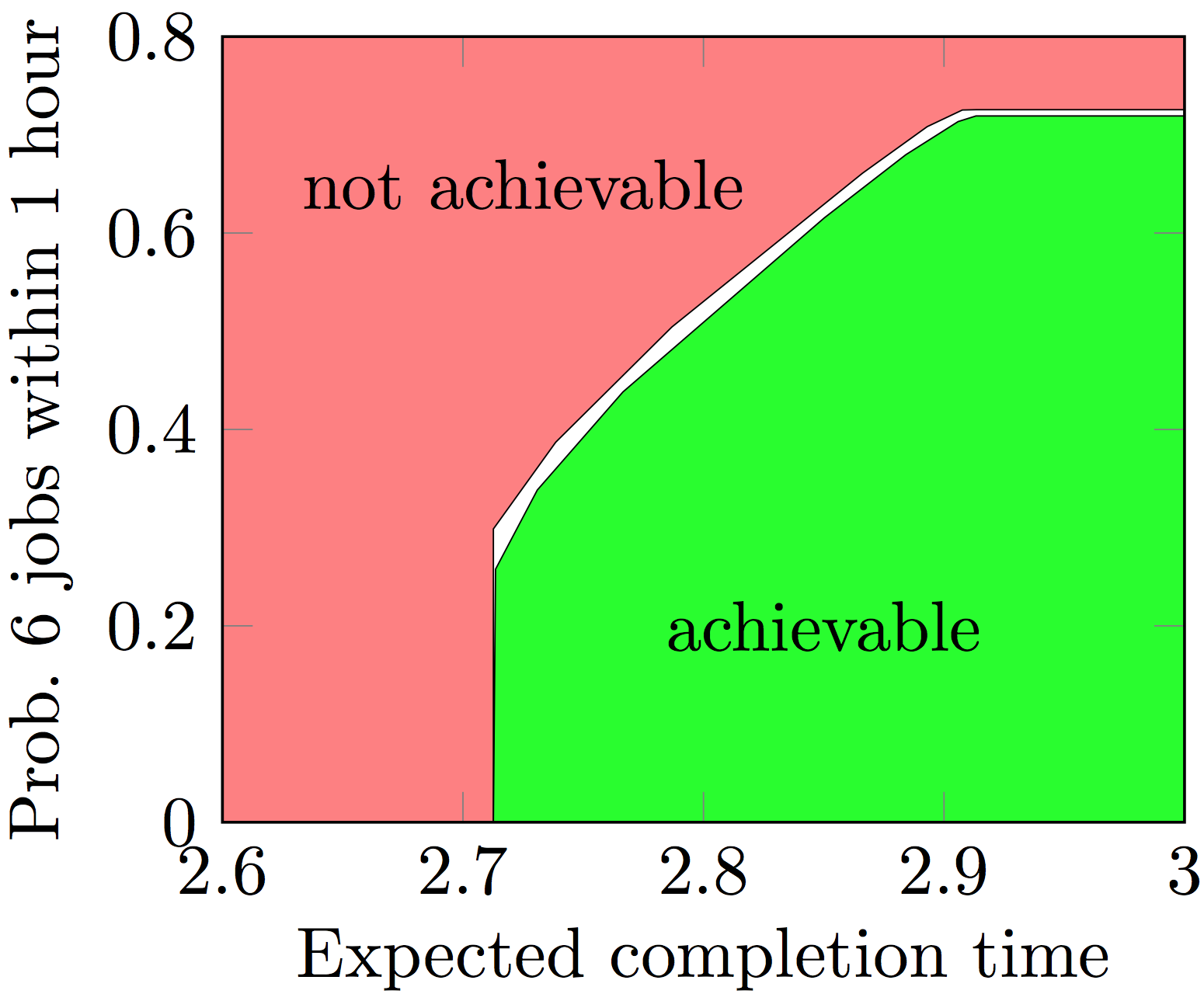
Download PRISM file for stochastic job scheduling (3 jobs and 2 servers)
// Stochastic Job Scheduling, based on []
// Encoding by Junges & Quatmann
// RWTH Aachen University
// Please cite Quatmann et al: Multi-objective Model Checking of Markov Automata
ma
const int N = 3;
const int K = 2;
const double x_j1 = 1.0;
const double x_j2 = 2.0;
const double x_j3 = 3.0;
formula is_running = r_j1 + r_j2 + r_j3 > 0;
formula num_finished = f_j1 + f_j2 + f_j3;
module main
r_j1 : [0..1];
r_j2 : [0..1];
r_j3 : [0..1];
f_j1 : [0..1];
f_j2 : [0..1];
f_j3 : [0..1];
<> (r_j1 = 1) -> x_j1 : (r_j1' = 0) & (r_j2' = 0) & (r_j3' = 0) & (f_j1' = 1);
<> (r_j2 = 1) -> x_j2 : (r_j1' = 0) & (r_j2' = 0) & (r_j3' = 0) & (f_j2' = 1);
<> (r_j3 = 1) -> x_j3 : (r_j1' = 0) & (r_j2' = 0) & (r_j3' = 0) & (f_j3' = 1);
[] (!is_running) & (num_finished = 2) & (f_j1 = 0) -> 1: (r_j1' = 1);
[] (!is_running) & (num_finished = 2) & (f_j2 = 0) -> 1: (r_j2' = 1);
[] (!is_running) & (num_finished = 2) & (f_j3 = 0) -> 1: (r_j3' = 1);
[] (!is_running) & (num_finished <= 1) & (f_j1 = 0) & (f_j2 = 0) -> 1: (r_j1' = 1) & (r_j2' = 1);
[] (!is_running) & (num_finished <= 1) & (f_j1 = 0) & (f_j3 = 0) -> 1: (r_j1' = 1) & (r_j3' = 1);
[] (!is_running) & (num_finished <= 1) & (f_j2 = 0) & (f_j3 = 0) -> 1: (r_j2' = 1) & (r_j3' = 1);
endmodule
init
r_j1 = 0 &
r_j2 = 0 &
r_j3 = 0 &
f_j1 = 0 &
f_j2 = 0 &
f_j3 = 0
endinit
label "all_jobs_finished" = num_finished=N;
label "half_of_jobs_finished" = num_finished=2;
label "slowest_before_fastest" = f_j1=1 & f_j3=0;
rewards "avg_waiting_time"
true : (N-num_finished)/N;
endrewards
Again, we assume that the file jobs03_2.ma is located in the current directory.
We obtain the data for tha Pareto plot as above by the following call:
$ storm --prism jobs03_2.ma --prop "multi(Tmin=? [ F \"all_jobs_finished\"], Pmax=? [ F<=(N/(4*K)) \"half_of_jobs_finished\"])" --multiobjective:precision 0.01 --multiobjective:exportplot plot/
--prop now contains a multi-objective query with two dimensions: A call for the expected time, and a maximum time-bounded probability.
Notice that for Markov automata, the algorithm necessarily can only approximate the result: --multiobjective:precision reflects the area that remains undecided.
--multiobjective:exportplot plot/ specifies that the directory plot will contain the Pareto-optimal points in a CSV format. The plot can be generated from this file.
More benchmarks and further details for multi-objective model checking can also be found in this repository.
Running Storm on JANI input
JANI models can be provided with the --jani <path/to/jani-file> option.
In case you also want to read the properties from the jani file, the option --janiproperty needs to be added.
Example 4 (Analysis of a rejection-sampling algorithm to approximate \(\pi\))
Here, we are going to analyze a model of an algorithm that approximates \(\pi\). It does so by repeated sampling according to a uniform distribution. While this model is a JANI model, the original model was written in the probabilistic guarded command language (pGCL) and has been translated to JANI. The JANI model and the original pGCL code is available from the JANI models repository.
Download original pGCL program
// Approximating Pi by Rejection Sampling / Monte Carlo.
// Automatically Generated by: storm-pgcl-BG
// Sebastian Junges; RWTH Aachen University
function approachPi() {
var {
int x := 0;
int y := 0;
int shots := 0;
int hits := 0;
}
while( shots <= 100 ) {
x := unif(-10,10);
y := unif(-10, 10);
if (x*x + y*y <= 10*10) {
hits := hits + 1;
}
shots := shots + 1;
}
}
Download JANI model of rejection-sampling algorithm
{
"actions": [],
"automata": [
{
"edges": [
{
"destinations": [
{
"assignments": [
{
"ref": "hits",
"value": 1
}
],
"location": "l5",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": true
},
"location": "l6"
},
{
"destinations": [
{
"assignments": [],
"location": "oob-shots",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"left": {
"left": {
"left": "shots",
"op": "+",
"right": 1
},
"op": ">",
"right": 101
},
"op": "∨",
"right": {
"left": {
"left": "shots",
"op": "+",
"right": 1
},
"op": "<",
"right": 0
}
}
},
"location": "l5"
},
{
"destinations": [
{
"assignments": [
{
"ref": "shots",
"value": {
"left": "shots",
"op": "+",
"right": 1
}
}
],
"location": "l0",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"left": {
"left": {
"left": "shots",
"op": "+",
"right": 1
},
"op": "≤",
"right": 101
},
"op": "∧",
"right": {
"left": {
"left": "shots",
"op": "+",
"right": 1
},
"op": "≥",
"right": 0
}
}
},
"location": "l5"
},
{
"destinations": [
{
"assignments": [],
"location": "l6",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"left": {
"left": {
"left": "x",
"op": "*",
"right": "x"
},
"op": "+",
"right": {
"left": "y",
"op": "*",
"right": "y"
}
},
"op": "≤",
"right": 100
}
},
"location": "l4"
},
{
"destinations": [
{
"assignments": [],
"location": "l5",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"exp": {
"left": {
"left": {
"left": "x",
"op": "*",
"right": "x"
},
"op": "+",
"right": {
"left": "y",
"op": "*",
"right": "y"
}
},
"op": "≤",
"right": 100
},
"op": "¬"
}
},
"location": "l4"
},
{
"destinations": [
{
"assignments": [
{
"ref": "y",
"value": -10
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -9
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -8
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -7
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -6
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -5
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -4
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -3
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -2
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": -1
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 0
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 1
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 2
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 3
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 4
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 5
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 6
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 7
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 8
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 9
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "y",
"value": 10
}
],
"location": "l4",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
}
],
"guard": {
"exp": true
},
"location": "l3"
},
{
"destinations": [
{
"assignments": [
{
"ref": "x",
"value": -10
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -9
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -8
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -7
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -6
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -5
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -4
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -3
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -2
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": -1
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 0
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 1
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 2
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 3
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 4
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 5
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 6
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 7
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 8
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 9
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
},
{
"assignments": [
{
"ref": "x",
"value": 10
}
],
"location": "l3",
"probability": {
"exp": {
"left": 1,
"op": "/",
"right": 21
}
}
}
],
"guard": {
"exp": true
},
"location": "l2"
},
{
"destinations": [
{
"assignments": [],
"location": "l1",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": true
},
"location": "l1"
},
{
"destinations": [
{
"assignments": [],
"location": "l2",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"left": "shots",
"op": "≤",
"right": 100
}
},
"location": "l0"
},
{
"destinations": [
{
"assignments": [],
"location": "l1",
"probability": {
"exp": 1
}
}
],
"guard": {
"exp": {
"exp": {
"left": "shots",
"op": "≤",
"right": 100
},
"op": "¬"
}
},
"location": "l0"
}
],
"initial-locations": [
"l0"
],
"locations": [
{
"name": "l6",
"transient-values": []
},
{
"name": "l5",
"transient-values": []
},
{
"name": "l4",
"transient-values": []
},
{
"name": "l3",
"transient-values": []
},
{
"name": "l2",
"transient-values": []
},
{
"name": "l1",
"transient-values": [
{
"ref": "_ret0_",
"value": true
}
]
},
{
"name": "l0",
"transient-values": []
},
{
"name": "oob-shots",
"transient-values": []
}
],
"name": "main",
"variables": [
{
"initial-value": 0,
"name": "shots",
"transient": false,
"type": {
"base": "int",
"kind": "bounded",
"lower-bound": 0,
"upper-bound": 101
}
},
{
"initial-value": 0,
"name": "y",
"transient": false,
"type": {
"base": "int",
"kind": "bounded",
"lower-bound": -10,
"upper-bound": 10
}
},
{
"initial-value": 0,
"name": "x",
"transient": false,
"type": {
"base": "int",
"kind": "bounded",
"lower-bound": -10,
"upper-bound": 10
}
}
]
}
],
"constants": [],
"jani-version": 1,
"name": "program_graph",
"restrict-initial": {
"exp": true
},
"system": {
"elements": [
{
"automaton": "main"
}
]
},
"type": "mdp",
"variables": [
{
"initial-value": 0,
"name": "hits",
"transient": true,
"type": "int"
},
{
"initial-value": false,
"name": "_ret0_",
"transient": true,
"type": "bool"
}
]
}
Again, we will assume that the file approx_pi_00100_010_full.jani is located in the current directory. Let’s see how many states the underlying MDP has. For the sake of illustration, we are going to use the hybrid engine for this example.
$ storm --jani approx_pi_00100_010_full.jani --engine hybrid
Storm 1.0.0
Command line arguments: --jani approx_pi_00100_010_full.jani --engine hybrid
Current working directory: ~/storm/build/bin
Time for model construction: 0.069s.
--------------------------------------------------------------
Model type: MDP (symbolic)
States: 254304 (108 nodes)
Transitions: 2018744 (663 nodes)
Choices: 254304
Reward Models: none
Variables: rows: 4 meta variables (20 DD variables), columns: 4 meta variables (20 DD variables), nondeterminism: 3 meta variables (3 DD variables)
Labels: 0
--------------------------------------------------------------
As we selected the hybrid engine, Storm builds the MDP in terms of a symbolic data structure ((MT)BDDs), hence the (symbolic) marker. For this representation, Storm also reports the sizes of the state and transition DDs in terms of the number of nodes.
The algorithm uses a sampling-based technique to approximate \(\pi\). More specifically, it repeatedly (100 times in this particular instance) samples points in a square and checks whether they are in a circle whose diameter is the edge length of the square (which is called a hit). From this, we can derive \(\pi \approx 4 \frac{hits}{100}\) (for more details, we refer to this explanation). We are therefore interested in the expected number of hits until termination of the algorithm. The program has a transient Boolean variable _ret0_ that marks termination of the pGCL program; this transient variable can be used as a label in properties:
$ storm --jani approx_pi_00100_010_full.jani --engine hybrid --prop "Rmax=? [F \"_ret0_\"]"
Storm 1.0.0
Command line arguments: --jani approx_pi_00100_010_full.jani --engine hybrid --prop Rmax=? [F "_ret0_"]
Current working directory: ~/storm/build/bin
Time for model construction: 0.067s.
--------------------------------------------------------------
Model type: MDP (symbolic)
States: 254304 (108 nodes)
Transitions: 2018744 (663 nodes)
Choices: 254304
Reward Models: hits
Variables: rows: 4 meta variables (20 DD variables), columns: 4 meta variables (20 DD variables), nondeterminism: 3 meta variables (3 DD variables)
Labels: 1
* _ret0_
--------------------------------------------------------------
Model checking property R[exp]max=? [F "_ret0_"] ...
Result (initial states): 72.60088512
Time for model checking: 23.496s.
Plugging this value in our formula yields \(\pi \approx 4 \frac{hits}{100} = 4 \frac{72.60088512}{100} \approx 2.90404\). Of course, this is a crude approximation, but it can be refined by adjusting the size of the circle and the number of samples (see the other instances of this model in the JANI models repository).
Running Storm on Benchmarks from the Quantitative Verification Benchmark Set
To run Storm on a benchmark from the Quantitative Verification Benchmark Set (QVBS) (say, for example, the model jobs, type:
$ storm --qvbsroot QCOMP_DIR/benchmarks --qvbs jobs
Storm 1.4.1 (dev)
Command line arguments: --qvbsroot QCOMP_DIR/benchmarks --qvbs jobs
Current working directory: ~
--------------------------------------------------------------
QVBS ma-Benchmark: Stochastic Job Scheduling (jobs) v1
3 instances:
*0 jobs.5-2.jani (117 states)
1 jobs.10-3.jani (16439 states)
2 jobs.15-3.jani (1896568 states)
3 properties:
*completiontime (exp-time)
*avgtime (exp-reward)
*prhalfdone (prob-reach-time-bounded)
--------------------------------------------------------------
Time for model input parsing: 0.004s.
Time for model construction: 0.031s.
--------------------------------------------------------------
Model type: Markov Automaton (sparse)
States: 117
Transitions: 251
Choices: 171
Markovian St.: 86
Max. Rate.: 6
Reward Models: avg_waiting_time
State Labels: 4 labels
* init -> 1 item(s)
* half_of_jobs_finished -> 20 item(s)
* deadlock -> 1 item(s)
* all_jobs_finished -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.000s.
--------------------------------------------------------------
Model type: Markov Automaton (sparse)
States: 117
Transitions: 251
Choices: 171
Markovian St.: 86
Max. Rate.: 6
Reward Models: avg_waiting_time
State Labels: 4 labels
* init -> 1 item(s)
* half_of_jobs_finished -> 20 item(s)
* deadlock -> 1 item(s)
* all_jobs_finished -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Model checking property "completiontime": T[exp]min=? [F "all_jobs_finished"] ...
Result (for initial states): 1.6
Time for model checking: 0.000s.
Model checking property "avgtime": R[exp]{"avg_waiting_time"}max=? [F "all_jobs_finished"] ...
Result (for initial states): 0.9
Time for model checking: 0.000s.
Model checking property "prhalfdone": Pmax=? [true U<=(5 / 8) "half_of_jobs_finished"] ...
Result (for initial states): 0.6099104835
Time for model checking: 0.000s.
Here, we assume that the QComp git repository has been cloned into the directory QCOMP_DIR. If you built Storm from source, you can also set the cmake option -DSTORM_LOAD_QVBS=ON which will automatically download the complete benchmark set during the build step, allowing you to omit the --qvbsroot QCOMP_DIR/benchmarks command line option.
The above command checks all available properties for the first instance of the model jobs. The model checking call is equivalent to invoking Storm on the respective JANI file. The output also indicates the other available instances and the available properties. You can append an instance index and a comma seperated list of property names to the command above:
$ storm --qvbsroot QCOMP_DIR/benchmarks --qvbs jobs 2 completiontime,avgtime
Storm 1.4.1 (dev)
Command line arguments: --qvbsroot QCOMP_DIR/benchmarks --qvbs jobs 1 'completiontime,avgtime'
Current working directory: ~
--------------------------------------------------------------
QVBS ma-Benchmark: Stochastic Job Scheduling (jobs) v1
3 instances:
0 jobs.5-2.jani (117 states)
*1 jobs.10-3.jani (16439 states)
2 jobs.15-3.jani (1896568 states)
3 properties:
*completiontime (exp-time)
*avgtime (exp-reward)
prhalfdone (prob-reach-time-bounded)
--------------------------------------------------------------
Time for model input parsing: 0.038s.
Time for model construction: 0.735s.
--------------------------------------------------------------
Model type: Markov Automaton (sparse)
States: 16439
Transitions: 61596
Choices: 30831
Markovian St.: 15416
Max. Rate.: 9
Reward Models: avg_waiting_time
State Labels: 3 labels
* init -> 1 item(s)
* deadlock -> 1 item(s)
* all_jobs_finished -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Time for model preprocessing: 0.002s.
--------------------------------------------------------------
Model type: Markov Automaton (sparse)
States: 16439
Transitions: 61596
Choices: 30831
Markovian St.: 15416
Max. Rate.: 9
Reward Models: avg_waiting_time
State Labels: 3 labels
* init -> 1 item(s)
* deadlock -> 1 item(s)
* all_jobs_finished -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Model checking property "completiontime": T[exp]min=? [F "all_jobs_finished"] ...
Result (for initial states): 2.45620076
Time for model checking: 0.018s.
Model checking property "avgtime": R[exp]{"avg_waiting_time"}max=? [F "all_jobs_finished"] ...
Result (for initial states): 1.285765668
Time for model checking: 0.011s.
Running Storm on explicit input
Sometimes, it is convenient to specify your model in terms of an explicit enumeration of states and transitions (for example if your model is generated by another tool). For this, Storm offers the explicit input format. Models in this format consist of (at least) two files and can be provided with the --explicit <path/to/tra-file> <path/to/lab-file> option. Additionally, the options --staterew <path/to/state-rewards-file> and --transrew <path/to/transition-rewards-file> can be used to specify state and transition rewards.
Example 4 (Analysis of an explicit model of the Knuth-Yao die)
Here, we take the same input model as for Example 1 of the PRISM input section. However, this time the input model is given in the explicit format.
Download explicit transition file of Knuth-Yao die
dtmc
0 1 0.5
0 2 0.5
1 3 0.5
1 4 0.5
2 5 0.5
2 6 0.5
3 1 0.5
3 7 0.5
4 8 0.5
4 9 0.5
5 10 0.5
5 11 0.5
6 2 0.5
6 12 0.5
7 7 1
8 8 1
9 9 1
10 10 1
11 11 1
12 12 1
Download explicit label file of Knuth-Yao die
#DECLARATION
init one done deadlock
#END
0 init
7 one done
8 done
9 done
10 done
11 done
12 done
Download explicit (transition) reward file of Knuth-Yao die
0 1 1
0 2 1
1 3 1
1 4 1
2 5 1
2 6 1
3 1 1
3 7 1
4 8 1
4 9 1
5 10 1
5 11 1
6 2 1
6 12 1
Again, we assume that all three files are located in the current directory. We proceed analogously to the example in the PRISM input section and start by loading the model:
$ storm --explicit die.tra die.lab --transrew die.tra.rew
Storm 1.0.0
Command line arguments: --explicit die.tra die.lab --transrew die.tra.rew
Current working directory: ~/storm/build/bin
Time for model construction: 0.001s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: (default)
Labels: 3
* deadlock -> 0 state(s)
* one -> 1 state(s)
* init -> 1 state(s)
choice labels: no
--------------------------------------------------------------
Note that in contrast to the PRISM input model, the explicit version of the Knuth-Yao die does not have symbolic variables. Therefore, we need to rephrase the properties from before. Computing the probability of rolling a one thus becomes
$ storm --explicit die.tra die.lab --transrew die.tra.rew --prop "P=? [F \"one\"]"
Storm 1.0.0
Command line arguments: --explicit die.tra die.lab --transrew die.tra.rew --prop P=? [F "one"]
Current working directory: ~/storm/build/bin
Time for model construction: 0.000s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: (default)
Labels: 4
* deadlock -> 0 state(s)
* done -> 6 state(s)
* one -> 1 state(s)
* init -> 1 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property P=? [F "one"] ...
Result (initial states): 0.1666666667
Time for model checking: 0.000s.
Unlike for PRISM and JANI models, there is no --exact mode for explicit input as it’s already imprecise because of floating point numbers.
Note that the model defines two labels one and done that can be used in properties. For reward properties, the only difference in property specification is that formulae must not refer to a specific reward model but rather to the implicit default one. This is because in the explicit input format, every model can have only up to one reward model and there is no way to specify its name in the input format. Consequently, computing the expected number of coin flips that are necessary until the simulated die has terminated with an outcome in {1, …, 6} can be done like this:
$ storm --explicit die.tra die.lab --transrew die.tra.rew --prop "R=? [F \"done\"]"
Storm 1.0.0
Command line arguments: --explicit die.tra die.lab --transrew die.tra.rew --prop P=? [F "one"]
Current working directory: ~/storm/build/bin
Time for model construction: 0.000s.
--------------------------------------------------------------
Model type: DTMC (sparse)
States: 13
Transitions: 20
Reward Models: (default)
Labels: 4
* deadlock -> 0 state(s)
* done -> 6 state(s)
* one -> 1 state(s)
* init -> 1 state(s)
choice labels: no
--------------------------------------------------------------
Model checking property R[exp]=? [F "done"] ...
Result (initial states): 3.666666667
Time for model checking: 0.000s.
Running Storm on GSPNs
The binary storm-gsnp handles Generalized Stochastic Petri Nets (GSPNs).
GSPNs can be analysed by first converting them to the JANI format and then analyzing the JANI model as shown before.
Running Storm on Pnpro input
Example 6 (Analysis of a GSPN)
We start by parsing a GSPN given in the pnpro format used by the GreatSPN editor. The GSPN models four dining philosophers.
Download GSPN model of dining philosophers
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
<!-- This project file has been saved by the New GreatSPN Editor, v.100 --><project name="Dining Philosophers" version="121">
<gspn name="Philosophers4">
<nodes>
<place marking="1" name="fork1" x="21.0" y="4.0"/>
<transition delay="lambda" delay-x="-0.5" delay-y="1.5" name="T0" rotation="0.7853981633974483" type="EXP" x="26.55" y="9.0"/>
<transition delay="lambda" name="T1" rotation="2.356194490192345" type="EXP" x="16.55" y="9.0"/>
<place marking="1" name="fork4" x="11.0" y="14.0"/>
<place marking="1" name="fork2" x="31.0" y="14.0"/>
<transition delay="lambda" delay-x="0.0" delay-y="1.5" name="T2" rotation="0.7853981633974483" type="EXP" x="16.55" y="19.0"/>
<transition delay="lambda" name="T3" rotation="2.356194490192345" type="EXP" x="26.55" y="19.0"/>
<place marking="1" name="fork3" x="21.0" y="24.0"/>
<place name="eating1" x="11.0" y="9.0"/>
<place label-y="-1.5" marking="1" name="thinking1" x="16.0" y="4.0"/>
<place label-y="-1.5" name="wait1" x="6.0" y="4.0"/>
<place label-y="-1.5" name="eating2" x="26.0" y="4.0"/>
<place marking="1" name="thinking2" x="31.0" y="9.0"/>
<place label-y="-1.5" name="wait2" x="36.0" y="4.0"/>
<place name="eating3" x="31.0" y="19.0"/>
<place marking="1" name="thinking4" x="11.0" y="19.0"/>
<place name="eating4" x="16.0" y="24.0"/>
<place marking="1" name="thinking3" x="26.0" y="24.0"/>
<place name="wait3" x="36.0" y="24.0"/>
<place name="wait4" x="6.0" y="24.0"/>
<transition delay="rho" delay-x="0.0" delay-y="1.5" name="T4" rotation="2.356194490192345" type="EXP" x="6.55" y="9.0"/>
<transition delay="rho" name="T5" rotation="2.356194490192345" type="EXP" x="36.55" y="19.0"/>
<transition delay="mu" delay-x="-0.5" name="T6" rotation="0.7853981633974483" type="EXP" x="36.55" y="9.0"/>
<transition delay="mu" delay-x="0.0" name="T7" rotation="0.7853981633974483" type="EXP" x="6.55" y="19.0"/>
<transition delay="mu" name="T8" type="EXP" x="11.55" y="4.0"/>
<transition delay="rho" name="T9" type="EXP" x="31.55" y="4.0"/>
<transition delay="mu" name="T10" type="EXP" x="31.55" y="24.0"/>
<transition delay="rho" delay-x="0.0" delay-y="1.5" name="T11" type="EXP" x="11.55" y="24.0"/>
<constant consttype="REAL" name="lambda" value="1" x="1.4375" y="2.0"/>
<constant consttype="REAL" name="mu" value="1" x="1.4375" y="3.0"/>
<constant consttype="REAL" name="rho" value="1" x="1.5" y="4.0"/>
</nodes>
<edges>
<arc head="fork4" kind="OUTPUT" mult-k="0.5" tail="T1"/>
<arc head="fork2" kind="OUTPUT" mult-k="0.5" tail="T0"/>
<arc head="fork3" kind="OUTPUT" mult-k="0.5" tail="T2"/>
<arc head="fork4" kind="OUTPUT" mult-k="0.18173828125000002" tail="T2"/>
<arc head="fork1" kind="OUTPUT" mult-k="0.5" tail="T1"/>
<arc head="fork1" kind="OUTPUT" mult-k="0.5" tail="T0"/>
<arc head="fork2" kind="OUTPUT" mult-k="0.5" tail="T3"/>
<arc head="fork3" kind="OUTPUT" mult-k="0.5" tail="T3"/>
<arc head="thinking1" kind="OUTPUT" mult-k="0.5" tail="T1"/>
<arc head="T8" kind="INPUT" mult-k="0.5" tail="thinking1"/>
<arc head="wait1" kind="OUTPUT" mult-k="0.5" tail="T8"/>
<arc head="T4" kind="INPUT" mult-k="0.5" tail="wait1"/>
<arc head="eating1" kind="OUTPUT" mult-k="0.5" tail="T4"/>
<arc head="T1" kind="INPUT" mult-k="0.5" tail="eating1"/>
<arc head="T4" kind="INPUT" mult-k="0.5" tail="fork4"/>
<arc head="T7" kind="INPUT" mult-k="0.5" tail="fork4"/>
<arc head="T5" kind="INPUT" mult-k="0.5" tail="fork2"/>
<arc head="T6" kind="INPUT" mult-k="0.5" tail="fork2"/>
<arc head="T0" kind="INPUT" mult-k="0.5" tail="eating2"/>
<arc head="thinking2" kind="OUTPUT" mult-k="0.5" tail="T0"/>
<arc head="T6" kind="INPUT" mult-k="0.5" tail="thinking2"/>
<arc head="wait2" kind="OUTPUT" mult-k="0.5" tail="T6"/>
<arc head="T9" kind="INPUT" mult-k="0.5" tail="wait2"/>
<arc head="eating2" kind="OUTPUT" mult-k="0.5" tail="T9"/>
<arc head="thinking3" kind="OUTPUT" mult-k="0.5" tail="T3"/>
<arc head="T10" kind="INPUT" mult-k="0.5" tail="thinking3"/>
<arc head="wait3" kind="OUTPUT" mult-k="0.5" tail="T10"/>
<arc head="T5" kind="INPUT" mult-k="0.5" tail="wait3"/>
<arc head="eating3" kind="OUTPUT" mult-k="0.5" tail="T5"/>
<arc head="T3" kind="INPUT" mult-k="0.5" tail="eating3"/>
<arc head="T2" kind="INPUT" mult-k="0.5" tail="eating4"/>
<arc head="thinking4" kind="OUTPUT" mult-k="0.5" tail="T2"/>
<arc head="T7" kind="INPUT" mult-k="0.5" tail="thinking4"/>
<arc head="wait4" kind="OUTPUT" mult-k="0.5" tail="T7"/>
<arc head="T11" kind="INPUT" mult-k="0.5" tail="wait4"/>
<arc head="eating4" kind="OUTPUT" mult-k="0.5" tail="T11"/>
<arc head="T8" kind="INPUT" mult-k="0.5" tail="fork1">
<point x="19.5" y="2.5"/>
<point x="14.0" y="2.5"/>
</arc>
<arc head="T9" kind="INPUT" mult-k="0.5" tail="fork1">
<point x="24.5" y="2.5"/>
<point x="30.0" y="2.5"/>
</arc>
<arc head="T11" kind="INPUT" mult-k="0.5" tail="fork3">
<point x="19.5" y="27.5"/>
<point x="14.5" y="27.5"/>
</arc>
<arc head="T10" kind="INPUT" mult-k="0.5" tail="fork3">
<point x="24.5" y="27.5"/>
<point x="30.0" y="27.5"/>
</arc>
</edges>
</gspn>
</project>
We convert the GSPN into a JANI file with the following command:
$ storm-gspn --gspnfile philosophers.pnpro --to-jani philosophers.jani --addprops --capacity 1
The argument --capacity <value> specifies the maximal capacity for all places.
Alternatively, it is possible to provide a file specifying the capacity for each place with --capacitiesfile <filename>.
The flag -addprops automatically adds some properties which are commonly used in Petri net analysis.
On the resulting JANI file we compute for example the maximal probability of reaching a deadlock within 10 time units:
$ storm --jani philosophers.jani --constants TIME_BOUND=10 --janiproperty MaxPrReachDeadlockTB
Storm 1.3.1 (dev)
Command line arguments: --jani philosophers.jani --constants TIME_BOUND=10 --janiproperty MaxPrReachDeadlockTB
Current working directory: ~/storm/build/bin
Time for model input parsing: 0.059s.
Time for model construction: 0.240s.
--------------------------------------------------------------
Model type: CTMC (sparse)
States: 34
Transitions: 89
Reward Models: none
State Labels: 3 labels
* deadlock -> 0 item(s)
* init -> 1 item(s)
* deadl -> 1 item(s)
Choice Labels: none
--------------------------------------------------------------
Model checking property "MaxPrReachDeadlockTB": Pmax=? [true U<=10 "deadl"] ...
Result (for initial states): 0.8547786624
Time for model checking: 0.016s.
For additional command-line options see the help for GSPNs with:
$ storm-gspn --help gspn